Vår første modell
I forrige post startet vi på veien opp et fjell av kunnskap fra statistikkens og maskinlæringens verden. Vi ble introdusert til konsepter som varians, ko-varians, standardavvik og korrelasjon. I denne posten skal vi ta enda et steg på vei opp dette fjellet. Som du forhåpentligvis husker, tok vi i forrige post på oss rollen som en karuselloperatør i et tivoli. Karusellen vi opererer krever at alle som tar den er over en gitt minimumshøyde (160 cm), men vi har mistet målebåndet vårt og har kun en vekt som hjelpemiddel.
Vi har allerede sett at det kan se ut som om det er en viss sammenheng mellom vekt og høyde, og vi har til og med beregnet en korrelasjon på 0.72 mellom vekt og høyde! Desverre var vi ikke i stand til å bruke denne informasjonen for å hjelpe oss til å ta en avgjørelse om vi skal la en person ta karusellen eller ikke når vi vet vekten til personen. Dette skal vi forsøke å gjøre noe med i dag!
Modellere høyde fra vekt
I dag skal vi prøve å utvikle noen modeller som kan hjelpe oss å forutsi høyden til en person, gitt at vi vet vekten. Hvis vi klarer å bygge en god nok modell, vil vi kunne bruke den til å hjelpe oss å velge hvem som får lov til å ta karusellen og hvem som er for lave.
Vi starter igjen med det samme datasettet som vi så i forrige post: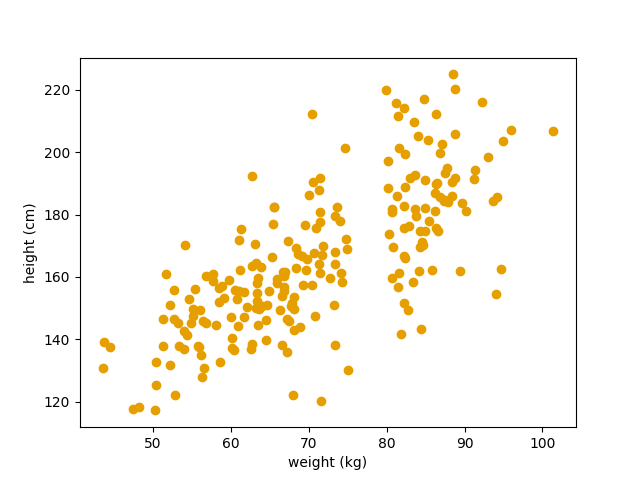 
Her plotter vi vekt (x-aksen) mot høyde (y-aksen).
Vi har vekt- og høydedata fra 221 personer. Dette datasettet ønsker vi nå å bruke til å bygge en statistisk/maskinlærings- modell som kan mates med en ny vektmåling og deretter spytte ut en prediksjon for hva høyden er. Men hvordan gjør vi det egentlig? Vel, vi kan jo tenke litt på hvordan vi selv modellerer slike ting i hodet. I mange tilfeller, hvis vi skal utføre en ny oppgave vi aldri har gjort før, så bruker vi erfaringer vi har fra andre oppgaver vi har gjort og som ligner. Kan vi ikke bruke en lignende tilnærming til dette problemet? For eksempel, hver gang vi måler en ny vekt, så kan vi finne den nærmeste vekten vi har i datasettet vårt og så se hvor høy den personen var. Deretter sier vi bare at denne nye vektmålingen korresponderer med samme høyde. La oss ta en kikk på hvordan det vil se ut.
Først må vi kode opp en slik modell, vi trenger to funksjoner. En funksjon beregner avstanden mellom to vektmålinger. Her kan vi bruke mange forskjellig mål på distanse, men vi velger Euklidsk distanse for enkelhets skyld. Deretter trenger vi også en funksjon som beregner distansen mellom en ny vektmåling og alle vektmålingene i datasettet vårt. Denne funksjonen skal også returnere høyden til den personen som hadde en vekt som var mest lik den nye vekten vi målte:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def euclidian_distance(w1: float = None, w2: float = None):
"""
Calculates the euclidian distance between two weight measurements w1 and w2
returns: the calculated distance
"""
return math.sqrt((w1-w2)**2)
def nearest_neighboor(new_weight: float= None):
distances = []
# Calculate distance between our new weight measurement and all other weight measurements we have in our data
for idx, person in df_w2h.iterrows():
# For each person in our dataset, we calculate the distance to the new weight and we store the height of this person
distances.append(np.array([euclidian_distance(new_weight, person.weight), person.height]))
# Sort the list of distances calculated
distances.sort(key = lambda x: x[0])
# Return the height of the person in our dataset that has the closest weight to the one we measured
return distances[0][1]
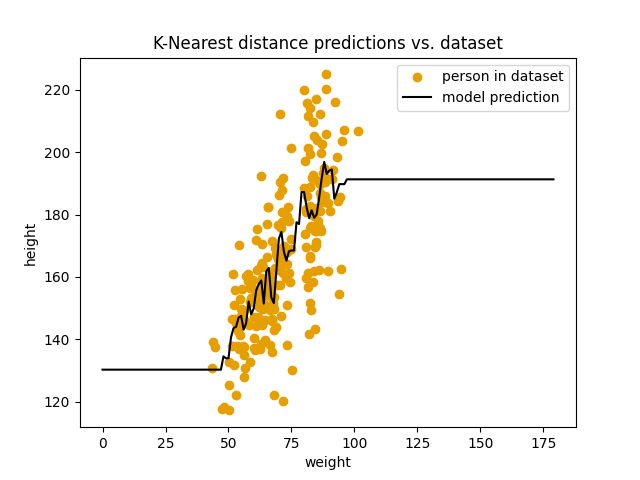
Over har jeg skrevet kode som gjør akkurat det vi ønsker. Vi kan nå visualisere resultatet fra denne koden. I bildet under kan vi se hvordan modellens prediksjoner (svart linje) passer med datasettet vårt. 
Her plotter vi modellens prediksjoner mot datasettet vårt.
Her synes jeg vi skal være ganske fornøyde med oss selv. Vi har klart å bygge en modell som faktisk kan gjøre prediksjoner og som kan hjelpe oss til å avgjøre om vi skal la en person få ta karusellen vår. Det er egentlig ganske kult! Men hvor bra fungerer egentlig modellen vår? Kan vi stole på prediksjonene den kommer med?
Evaluering av modellen
Å svare på det er egentlig veldig utfordrende og et stort felt innenfor statistikk og maskinlæring. Heldigvis må man ikke ha lest alt det for i det minste å kunne starte jobben med å evaluere modellen. Så hvordan kan vi si noe om modellens prediksjoner? En måte kan jo være å bruke en liten andel av datasettet vårt som verifikasjonsdata. Her kan vi f.eks velge ut 10% av personene vi har i datasettet og evaluere hvor godt modellen vår predikerer høyden på disse, gitt vektmålingen vi har. Hvordan kvantifiserer vi “hvor godt” modellen predikerer? Det kan variere ut ifra problemet vårt, men i dette tilfellet kan vi for eksempel bruke avviket mellom modellens høydeprediksjon og den faktiske høyden til personen. Vi trenger jo ikke å gjøre det for vanskelig heller.
La oss skrive kode som gjør dette for oss:
1
2
3
4
5
6
7
8
9
10
verification_weights = pd.DataFrame(df_w2h.sample(int(len(df_w2h)*0.1)))# Sample verification data
dataset_without_verification_weights = df_w2h.drop(verification_weights.index) # Remove the sample from the data used to generate predictions
# Use our functions to get the nearest weight in our dataset for every weight in our verification data
predictions = [nearest_neighboor(dataset_without_verification_weights, wt[1].weight) for wt in verification_weights.iterrows()]
for idx, vp in enumerate(verification_weights.iterrows()):
print(f'pred: {predictions[idx]:.2f}, true: {vp[1].height:.2f}')
Når vi kjører denne koden får vi ut en liste med prediksjoner, sanne verdier og avviket mellom prediksjonen og den sanne verdien:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
pred: 193.35, true: 184.83, difference: 8.52
pred: 144.55, true: 152.24, difference: -7.69
pred: 178.10, true: 161.23, difference: 16.88
pred: 182.46, true: 177.08, difference: 5.38
pred: 182.46, true: 166.37, difference: 16.09
pred: 132.57, true: 125.38, difference: 7.19
pred: 150.94, true: 159.80, difference: -8.86
pred: 179.62, true: 167.98, difference: 11.65
pred: 166.69, true: 199.46, difference: -32.77
pred: 161.02, true: 144.65, difference: 16.38
pred: 167.33, true: 144.04, difference: 23.28
pred: 171.61, true: 146.01, difference: 25.61
pred: 166.69, true: 188.88, difference: -22.19
pred: 185.92, true: 215.71, difference: -29.79
pred: 137.17, true: 147.16, difference: -9.99
pred: 189.93, true: 212.31, difference: -22.38
pred: 146.67, true: 155.96, difference: -9.29
pred: 145.13, true: 137.85, difference: 7.28
pred: 203.73, true: 162.59, difference: 41.14
pred: 150.63, true: 151.81, difference: -1.18
pred: 190.96, true: 217.13, difference: -26.17
pred: 153.42, true: 149.64, difference: 3.78
Men vi ønsker oss gjerne bare ett tall som sier oss noe om hvor god modellen er. For å gjøre det kan vi jo ta gjennomsnittet av alle avvikene!
1
2
3
4
5
6
7
8
# Calculate average difference
def avg_diff(predictions, test_data):
differences = []
for idx, vp in enumerate(test_data.iterrows()):
differences.append(predictions[idx]-vp[1].height)
return sum(differences)/len(differences)
print(avg_diff(predictions, verification_weights))
Som gir oss:
1
0.59
Men kan det stemme da?! Vi ser jo at de aller fleste avvik vi har er mye større enn $\pm 0.59$ cm. Hva gikk galt? Jo, igjen har vi kommet borti dette med at forskjellig fortegn utligner hverandre. Så hvordan unngår vi det? Vi kan gjøre som sist! Vi kvadrerer først og deretter tar vi kvadratroten av gjennomsnittet av de kvadrerte avvikene:
1
2
3
4
5
6
7
8
# Calculate root squared average distance
def rms_diff(predictions, test_data):
differences = []
for idx, vp in enumerate(test_data.iterrows()):
differences.append((predictions[idx]-vp[1].height)**2)
return math.sqrt(sum(differences)/len(differences))
print(rms_diff(predictions, verification_weights))
Som nå gir oss:
1
19.1
Altså bommer modellen i gjennomsnitt med rundt 19.1 cm i prediksjonene sine. Det er jo ikke veldig ille, men kan vi forbedre det? Ja det tror jeg vi kan.
La oss forbedre modellen vår
I modellen vår så langt, så ser vi kun på den nærmeste personen i datasettet vårt, men hva om vi er veldig uheldig og den nærmeste personen er unormalt lav eller unormalt høy for vekten sin. Da vil jo modellen predikere en unormalt lav eller høy verdi også. Hvis vi tar en titt på prediksjonene våre igjen, så ser vi at modellen gjøre et stort hopp mellom ca 75kg og 80kg. Her har vi nettopp et slikt tilfelle, der den nærmeste målingen vi har på litt over 75 kg er unormalt lav, mens den nærmeste målingen nært 80 kg er unormalt høy. Modellen tror med andre ord at en typisk person på 75kg er ca. 130 cm, mens om personen er bare 5 kg tyngre er den nesten 220 cm. Det kan umulig stemme. Hvordan kan vi unngå det?
En ting vi kan gjøre er jo å bruke flere enn en person fra datasettet vårt hver gang vi gjør en prediksjon. Hva om vi f.eks skriver om modellen slik at den bruker gjennomsnittshøyden av de 5 nærmeste vektmålingene som prediksjon. La oss se hva som skjer da:
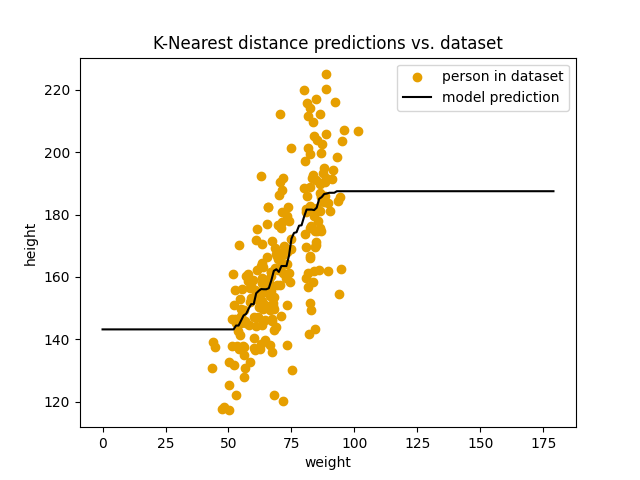
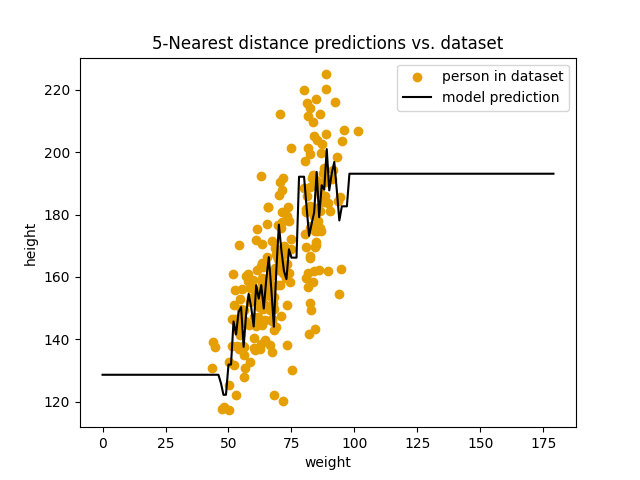Her plotter vi modellen som bruker de 5 nærmeste målingene for prediksjon mot datasettet vårt.
Umiddelbart ser vi en stor forskjell! Modellen virker mye mindre påvirket av unormalt høye og lave personer. Men hvordan ser avvikene ut? Vi kan kjøre koden vår igjen:
1
2
3
# Use our functions to get the nearest weight in our dataset for every weight in our verification data
five_nearest_predictions = [five_nearest_neighboor(dataset_without_verification_weights, wt[1].weight) for wt in verification_weights.iterrows()]
print(rms_diff(five_nearest_predictions, verification_weights))
Og da får vi:
1
16.9
$k$-nærmeste nabo ($k$-nearest neighboor)
Så ved å øke antallet personer vi bruker fra datasettet vårt for hver prediksjon har vi klart å forbedre modellens prestasjon. Veldig kult! Så la oss igjen tenke litt på hva modellen vår gjør: For hver vektmåling modellen skal predikere en høyde, så lager den på en måte et nabolag av vektmålinger fra datasettet vårt. I dette nabolaget velger den de 5 nærmeste naboene og beregner gjennomsnittshøyden for disse 5 naboene. Dette blir høyden modellen predikerer for den nye vektmålingen. Vi kan generalisere denne modellen til å kunne bruke et arbitrært antall naboer for beregningen også. La oss kalle antallet naboer vi bruker $k$. Vi kan utvide koden vi har skrevet slik:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
def k_nearest_neighboor(dataset, new_weight: float= None, k: int = 1):
distances = []
# Calculate distance between our new weight measurement and all other weight measurements we have in our data
for idx, person in dataset.iterrows():
# For each person in our dataset, we calculate the distance to the new weight and we store the height of this person
distances.append(np.array([euclidian_distance(new_weight, person.weight), person.height]))
# Sort the list of distances calculated
distances.sort(key = lambda x: x[0])
# Select the five nearest measurements
k_nearest = np.concatenate([distances[:k]], axis=1)
# Return the height of the person in our dataset that has the closest weight to the one we measured
return np.mean(k_nearest[:,1])
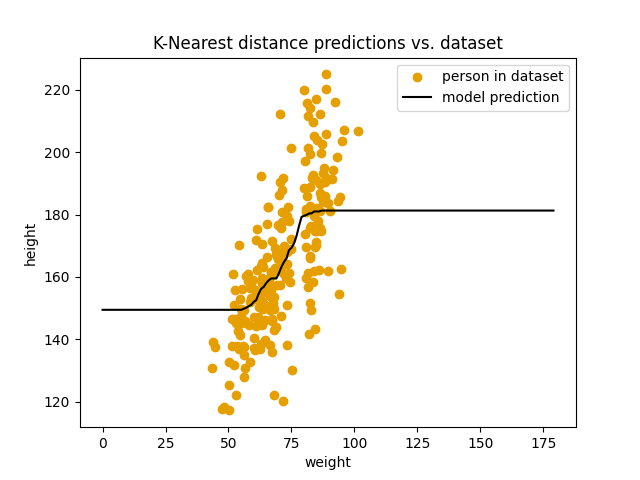
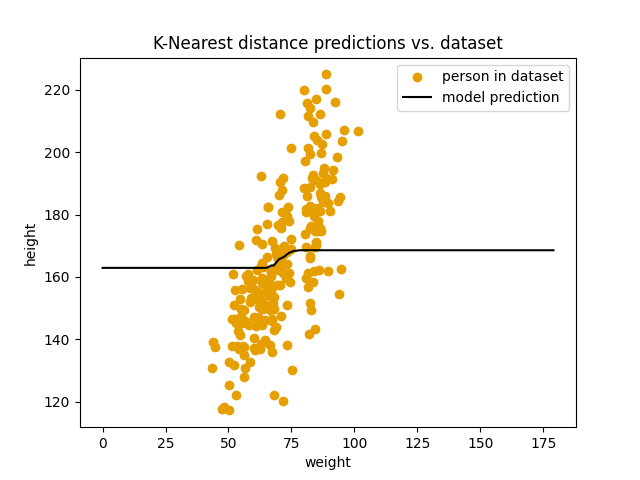
Denne modellen bruker altså de $k$ nærmeste naboene for en ny vektmåling for å predikere høyden. Så modellene vi brukte tidligere med $k=1$ og $k=5$ er bare spesielle instanser av denne mer generelle modellen. Og som du kanskje har gjettet, så er dette en modell som ofte brukes i reelle applikasjoner! Det generelle navnet er $k$-nærmeste nabo ($k$-nearest neighboor). Dette er en overraskende god modell med tanke på hvor enkel den er. Og den er ofte en veldig god modell å starte fra når vi skal modellere et problem. Men den har også sine begrensinger. La oss se på hva som skjer når vi øker $k$:
$k$ = 10: 
1
score: 17.90
$k$ = 50: 
1
score: 17.11
$k$ = 100: 
1
score: 17.39
$k$ = 200: 
1
score: 25.53
$k$ = 221 (alle datapunktene):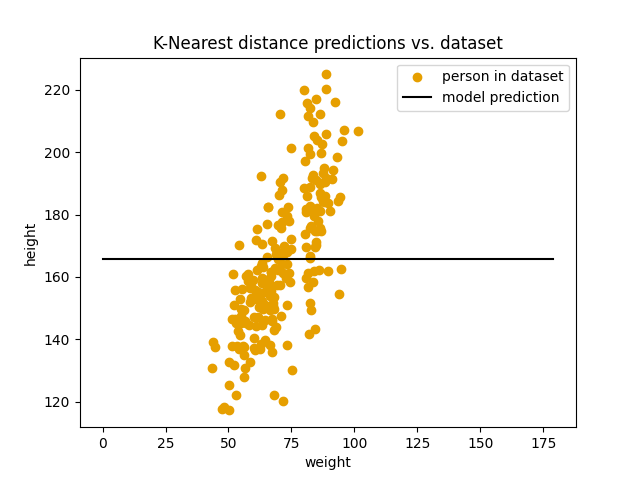 
1
score: 25.53
Modellen blir ikke bedre av å øke $k$. Den blir faktisk verre og verre. Det vi ser er at modellen gradvis nærmer seg en flat linje som ligger nøyaktig på gjennomsnittshøyden i datasettet vårt. Vi kan også verifisere dette med kode:
1
2
3
4
5
6
avg_height = np.round(df_w2h.height.mean(), 3)
all_predictions_equal = True
for i, prediction in enumerate(predictions):
if np.round(prediction, 3) != avg_height:
all_predictions_equal = False
print(f'All precitions are equal to the dataset average height: {all_predictions_equal}')
Dette gir oss outputen:
1
All precitions are equal to the dataset average height: True
Så modellen ender til slutt opp med bare å predikere gjennomsnittshøyden i datasettet vårt for enhver vektmåling om vi setter $k$ til en for høy verdi. $k$ er altså noe vi må justere og tilpasse for å finne den beste versjonen av $k$-nærmeste nabo modellen. En annen ting vi kan justere i modellen vår er hvordan vi kombinerer naboene. I modellen vi har brukt her beregner vi gjennomsnittet av høyden til naboene våre og bruker det som prediksjon. Men det finnes mange andre måter å gjøre dette på. For eksempel, hvis vi havner i en situasjon hvor den femte naboen er mye lengre unna enn de fire andre naboene vi finner, er det kanskje urimelig å la den påvirke resultatet like mye som de andre fire. For å gjøre noe med det kunne vi for eksempel vektet bidraget til hver nabo basert på hvor langt unna den er. Dette er en av mange måter man kan utvide $k$-nærmeste nabo modellen for å tilpasse den forskjellige problemer vi møter på.
Dette en kanskje en av de viktigste erfaringene jeg tror du kan trekke ut fra hele serien her. Alle modeller vi kommer til å se på har mange måter vi kan tilpasse dem vårt spesifikke problem på. Du vil ofte få resultater som generaliserer bedre til ny data (bedre modeller) om du tilpasser en enkel modell i stedet for å hoppe direkte til en avansert modell. Om du husker det, og gradvis forbedrer modellene dine når du selv skal modellere problemer, tror jeg du vil bygge bedre modeller som samtidig er enklere å forstå og bruke!
Og her tror jeg vi sier stopp for denne posten. I neste post skal vi se på hvordan vi tilnærme oss karusellproblemet vårt med å bruke en annen modell. Så ikke vær redd. Vi har langt igjen før vi nærmer oss toppen av fjellet.
Kode
Koden for denne posten finnes her.
Endringslogg
Under følger en endringslogg som viser hvilke deler av denne posten som er endret til hvilket tid. Enkle skrivefeil og den slags ting vil ikke bli logget, men jeg vil etterstrebe å logge alle meningsfulle endringer i posten.