Hvor bra passer modellen?

I forrige post kom vi ett steg nærmere å ha en modell som kan hjelpe oss med å avgjøre om vi kan la en person ta karusellen vår kun ved å måle personens vekt og bruke denne til å forutsi hvor høy personen er. Men vi er fortsatt ikke helt fornøyde.

La oss først, igjen, ta en kikk på dataen vår: 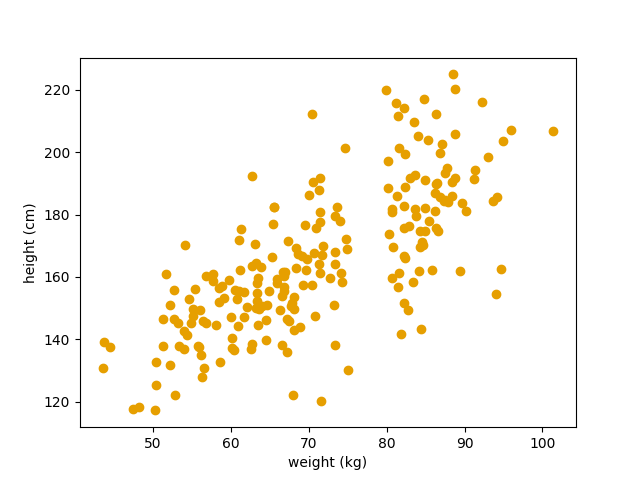Her plotter vi vekt (x-aksen) mot høyde (y-aksen).

I forrige post fant vi at linjen $Y = 71.94 + 1.32X$ var den linjen som passet aller best til dataen vår. Under ser vi igjen hvordan den linjen ser ut.

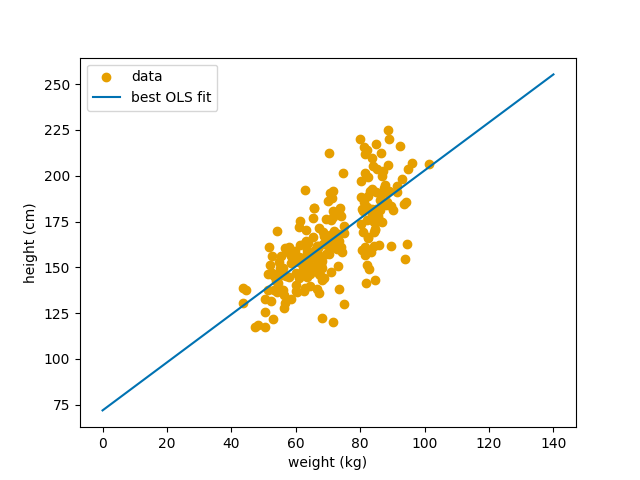Den beste OLS linjen plottet mot datasettet vårt.

I forrige post så vi deretter på hvor bra denne typen modell fungerte, ved å beregne gjennomsnittlig avvik fra høydene i et test-datasett. Vi fant at modellen vår gjorde det mye bedre enn $k$-nærmeste nabo modellen, men hvor bra passer egentlig modellen vår til dataen? Dette er jo et interessant spørsmål å stille seg. Selv om vi har funnet at modellen vår er bedre enn $k$-nærmeste nabo modellen, så vet vi egentlig ikke noe særlig om hvor god modellen vår faktisk er. Det kunne jo være at $k$-nærmeste nabo modellen vår var en utrolig dårlig modell og at å slå den var en veldig lett oppgave. Og at modellen vi nå har, derfor også er en dårlig modell. Så hvordan kan vi gå frem for å få litt peiling på hvor god modellen vår faktisk er?

Det første vi kan gjøre er, enkelt nok, å se på modellen plottet oppå dataen vår, slik vi har gjort over. En veldig dårlig modell ville vi avsløre ved ren inspeksjon. Den vil rett og slett ikke se ut som om den passer til dataen vår. Så allerede nå kan vi jo si at modellen ikke er en katastrofe. Det er jo betryggende. Men finnes det andre måter vi kan vurdere hvor godt modellen vår passer dataen vår? Ja det gjør det! Som du kanskje husker fra forrige post, så snakket vi om noe vi kalte residualer. Residualet er forskjellen mellom en observert verdi og en estimert verdi. Ja, veldig behjelpelig… Se for deg at du måler en vekt. Deretter bruker du modellen til å forutsi høyden til personen med denne vekten. Hvis vi så også faktisk måler høyden til personen, kan vi sammenligne modellens prediksjon med den faktiske målingen. Forskjellen på modellens prediksjon (estimatet) og den målte høyden (observasjonen) er residualet. Hvis vi kaller observasjonen $y_i$ og estimatet $\hat{y_i}$, i statistikk bruker vi ofte en hatt $\hat{}$ for å markere estimater, så kan vi definer residualet slik: \(\begin{equation} \text{residual} = y_i - \hat{y}_i \end{equation}\) Hvor $i$ indikerer hvilken måling blant $N$ målinger, slik at $i \in [1, 2, \ldots, N]$.

Vi kan med andre ord beregne residualet mellom modellen og hvert punkt i datasettet vårt. Vi kan deretter plotte disse residualene mot modellprediksjonene. Det har jeg gjort under: 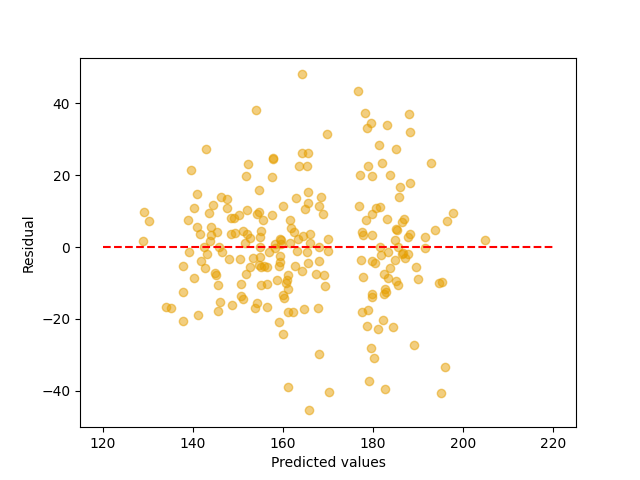Vi plotter residualene våre med residual langs y-aksen og prediksjonsverdien langs x-aksen. Vi markerer også nullinjen med en stiplet rød linje. Det er denne vi måler i mot.

Et slikt plott kalles et residualplott (residual plott). Det er et godt hjelpemiddel for å avgjøre hvor godt en modell passer til dataen vår. Med en perfekt modell vil man få et residualplott som ser helt tilfeldig fordelt ut rundt den røde stiplede linjen. Det er ingen antydning til mønster når vi beveger oss langs x-aksen. For ordens skyld har jeg plottet et “perfekt” residualplott under. Som du ser, er det ikke noe tydelig mønster for hvordan residualene fordeler seg i det perfekte plottet. Det er mindre og større avvik, men ikke noe tydelig mønster. Når vi så ser tilbake til residualplottet vi har for modellen vår, ser vi noe litt annet. Det kan se ut som om residualene vokser når vi nærmer oss 160. Hva betyr det?

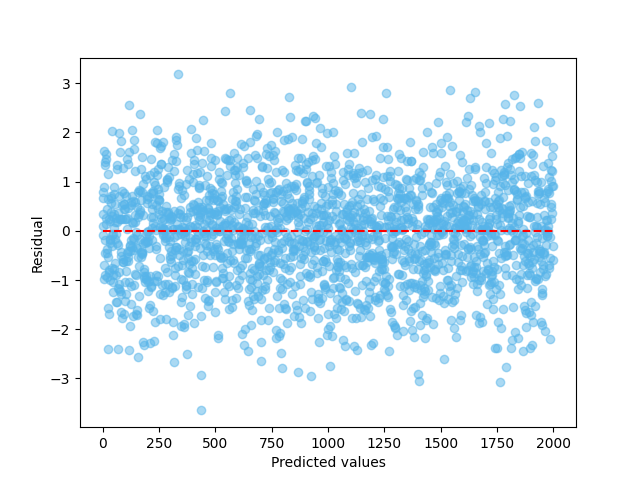Vi sampler fra en normaldistribusjon for å generere et “perfekt” residualplott.

Definisjonen av en modell

For å kunne svare fullgodt på dette, må vi først ta en nærmere kikk på hva det er vi kaller en modell. Da må vi starte med å se på hvordan dataen vår oppstår. Her ber jeg deg om å tillate at jeg later som om vi ikke genererte karuselldataen vår, men at vi faktisk målte den. Når vi gikk frem for å lage karuselldatasettet, så gjorde vi et tilfeldig utvalg av 221 personer. Vi startet med en liste over alle mennesker som bor i Norge, og brukte en eller annen prosess for å velge personer fra denne listen. Her er det viktig at prosessen som brukes er helt tilfeldig, slik at vi får det vi kaller et representativt utvalg. Det er et utvalg av 221 personer som er en god representasjon av den generelle befolkningen på 5.6 millioner mennesker. La oss si at vi i vår karuselldata har gjort dette perfekt! Dataen vår på 221 personer er en perfekt representasjon av befolkningen vi ønsker å finne ut sammenhengen mellom vekt og høyde om.

Da starter vi med å måle både vekt og høyde per person i utvalget vårt. Hver person går opp på en vekt og stiller seg inntil en vegg, slik at vi kan måle både vekt og høyde, på samme måte for alle personer. Vi skriver så ned det vi måler og dermed har vi datasettet vi ønsket oss. Men hvorfor lagde vi akkurat dette datasettet? Hvorfor brukte vi vekt for å kunne si noe om høyde? Jo, hvis du husker tilbake til [første post}(https://enklypesalt.com/posts/correlation/), så antok vi at det var en sammenheng mellom økende høyde og økende masse på en generell menneskekropp. Altså, jo høyere en person er, jo tyngre er den, på generell basis. Vi gjorde også noen enkle evalueringer av datasettet vårt for å se om det var en positiv korrelasjon mellom vekt og høyde. Det var det jo. Ettersom korrelasjon fungerer begge veier, betyr dette at økt vekt også er korrelert med økt høyde. Altså kan det kanskje være mulig å si noe om en persons høyde dersom vi kjenner vekten deres. Vi antar altså at høyde kan modelleres som en /funksjon/ av vekt, slik:

\[\begin{equation} \text{høyde} = f(\text{vekt}) \end{equation}\]

Vi tenker altså at det finnes en funksjon, $f$, som kan gi oss høyden til en person, dersom vi mater den med vekten. Vi har til nå sett på to funksjoner for å gjøre dette. $k$-nærmeste nabo og lineær regresjon. Det beste vi har funnet til nå er lineær regresjon. Her antar vi altså at funksjonen vår $f(\text{vekt}) = \beta_0 + \beta_1 \text{vekt}$, eller mer generelt: $f(x) = \beta_0 + \beta_1 x$. Men vi har glemt én ting her. Er det rimelig å anta at vi utførte en perfekt måling for alle personene da vi lagde datasettet vårt? Kan vi ikke ha bommet med et par millimeter på høyden? Eller kan ikke personene ha stått med litt forskjellig holdning da vi målte høyden? Jo det må vi nesten anta. Altså har det sneket seg inn noe usikkerhet rundt hver måling, eller støy. Vi kan derfor se for oss at hver eneste måling er summen av den faktiske høyden personen har, hvis man kunne måle den perfekt, og støy fra målingsprosessen vår. Det kan vi skrive slik: $\text{Måling} = \text{Signal} + \text{Støy}$. Hvor signalet er en perfekt måling, og støy er usikkerhet i målingsprosessen vår.

Vi kan derfor skrive om modellen vår slik: \(\begin{equation} \text{høyde} = f(\text{vekt}) + \epsilon \end{equation}\)

Hvor $\epsilon$ er støyen fra målingsprosessen vår. Men hvis vi nå antar at målingsprosessen vår fortsatt er veldig god, er det rimelig å anta at det ikke er noen systematisk støy i dataen vår. Altså, at vi ikke konsekvent måler en person litt for lav, eller at vi ber dem stå på en spesiell måte som farger målingen vår. Da kan vi også anta at målestøyen vår er normalfordelt, med et gjennomsnitt på 0. Altså er den gjennomsnittlige målefeilen vår 0, men for hver enkelt person vil den variere litt. Vi kan skrive dette som: $\epsilon \sim \mathcal{N}(0, \sigma^2)$. Hvor $\sigma^2$ er standardavviket i støyen, eller hvor mye den varierer i gjennomsnitt. Modellen vår for høyde ser nå altså slik ut:

\[\begin{equation} \text{høyde} = f(\text{vekt}) + \epsilon, \epsilon \sim \mathcal{N}(0, \sigma^2) \end{equation}\]

Generelt får vi da: \(\begin{equation} y = f(x) + \epsilon, \epsilon \sim \mathcal{N}(0, \sigma^2) \end{equation}\)

Så hvordan henger dette sammen med hvor godt modellen vår passer til dataen vår? Jo nå kan vi se tilbake på hvordan vi definerte et residual:

\[\begin{equation} r_i = y_i - \hat{y}_i \end{equation}\]

Der $\hat{y}_i$ er estimatet fra modellen vår. Dette kan vi skrive om, ved å bruke den generelle modelln vår over, slik: \(\begin{equation} \begin{aligned} r_i = (f(x_i) + \epsilon_i) - \hat{y}_i \\ r_i = f(x_i) - \hat{y}_i + \epsilon_i \end{aligned} \end{equation}\)

Og det er nå vi ser noe interessant. I den siste ligningen over, ser vi at hvis vi har et perfekt estimat, altså at $\hat{y}_i = f(x_i)$, så får vi at $r_i = \epsilon_i$ fordi $f(x_i) - \hat{y}_i = 0$. Det betyr også at residualene våre skal være normalfordelte, men gjennomsnitt 0 og standardavvik $\sigma^2$. Med en perfekt modell har vi altså $r \sim \mathcal{N}(0, \sigma^2)$. Dette er forklaringen på hvorfor vi forventer at det ikke skal være noe mønster i et residualplott for en perfekt modell, fordi for en perfekt modell vil residualet bare være støyen fra måten vi målte dataen vår på i første omgang!

Så når vi nå ser at residualplottet vårt ikke ser normalfordelt ut for den lineære modellen vi har utviklet har vi all grunn til å tro at det er noe feil med modellen vår. Det er med andre ord mulig å lage en bedre modell!

Kvantifikasjon av hvor godt modellen passer dataen vår

Dette er jo vel og bra, vi kan bruke residualplott til visuelt å evaluere hvor godt modellen vår passer til dataen vår. Men hva nå om vi har to modeller. Hvilken av disse modellene våre passer best til dataen? Vi har jo tidligere sett at vi kan beregne prediksjonsprestasjonen til modellene og sammenligne disse, men kan vi sammenligne hvor godt de passer dataen vår også? Vi kunne jo sammenlignet residualplottene til de to modellene, men det blir fort kronglete og gjerne subjektivt. Vi ønsker oss derfor et mer objektiv mål på dette. Gjerne et tall, slik vi fikk for prediksjonsprestasjon. Så hvordan kan vi få til det?

Vi burde åpenbart starte med residualene våre. Hvis vi summerer disse får vi et tall på det totale residualet for modellen vår. Men ikke glem at vi må kvadrere dette for å unngå at fortegn utligner hverandre. Vi kan da skrive dette som: \(\begin{equation} \text{Residual Kvadratsum} = \sum_{i=1}^N r_i^2 = \sum_{i=1}^N (y_i - \hat{y}_i)^2 \end{equation}\)

Vi kaller dette residual kvadratsummen (residual sum of squares) i statistikk. Men dette gir oss jo bare et tall som kan variere utrolig mye. Så det er veldig vanskelig å si hva en god residual kvadratsum er. Kan vi finne en måte å skalere dette tallet slik at det istedet ligger mellom $[0, 1]$ slik at 0 betyr at modellen er totalt feil og 1 betyr en perfekt modell. Ja det kan vi! Vi trenger først en måte å skalere residual kvadratsummen til $[0, 1]$. Det kan vi gjøre ved å dele det med den verst tenkelige residualsummen man kan se for seg. Men hva er den? Hvis vi ser for oss en modell som bare predikerer gjennomsnittshøyden for alle målingene våre, så har vi en veldig dårlig modell. Da er modellen definert slik: \(\begin{equation} \hat{y}_i = \bar{y} \end{equation}\)

For den modellen blir residualet kvadratsummen slik $\text{Residual Kvadratsum} \sum_{i=1}^N (y_i - \bar{y})^2$. Dette kaller vi gjerne den totale kvadratsummen (total sum of squares) i statistikk. Vi kan nå dele residual kvadratsummen på den totale kvadratsummen for å få et tall mellom $[0, 1]$ som angir hvor godt modellen passer dataen vår: \(\begin{equation} \text{hvor godt modellen passer dataen} = \frac{SS_{res}}{SS_{tot}} \end{equation}\)

Her har jeg brukt $SS_{res}$ for å representere residual kvadratsummen ($\text{Sum of Squares}{res}$) og $SS{tot}$ for å representere den totale kvadratsummen $\text{Sum of Squares}{tot}$. Men vi har fortsatt ett problem. Hvis $SS{res} = $SS_{tot}$, så blir jo dette regnestykket $1$ og hvis vi har en perfekt modell ($SS_{res} = 0$), så får blir regnestykket vårt $0$. Vi får nøyaktig det motsatte av hva vi ønsket oss. En perfekt modell får score $0$ og den verst tenkelige modellen får score $1$. Det er heldigvis lett å fikse ved å starte med $1$ og trekke fra regnestykket vårt, slik: \(\begin{equation} R^2 = 1 - \frac{SS_{res}}{SS_{tot}} \end{equation}\)

Da får vi en metrikk som gir score $1$ til en perfekt modell og $0$ til en verst tenkelig modell! Denne metrikken kalles $R^2$ i statistikken, eller “Coefficient of Determination” og brukes svært ofte som et mål på hvor godt modellen passer dataen vår. Så hva er egentlig $R^2$ for den lineære modellen vi har utviklet så langt? Heldigvis har noen skrevet koden som kan utføre denne beregningen for oss allerede, så vi trenger bare å kjøre denne koden:

from sklearn.metrics import r2_score
observations = [obs[1].height for obs in df_w2h.iterrows()]

print(f"{r2_score(observations, predictions):.3f}")

Som gir oss:

0.525

Også her ser vi at det er ganske mye å hente på å prøve å videreutvikle modellen vår. Det skal vi imidlertid se mer på i neste post.

Kode

Koden for denne posten finnes her.

Endringslogg

Under følger en endringslogg som viser hvilke deler av denne posten som er endret til hvilket tid. Enkle skrivefeil og den slags ting vil ikke bli logget, men jeg vil etterstrebe å logge alle meningsfulle endringer i posten.