En strek er også en modell
I forrige post bygget vi vår første modell for å hjelpe oss å løse problemet med å finne ut hvem som får lov til å ta karusellen vår, gitt vekten deres. Vi utviklet en $k$-nærmeste nabo modell og utviklet en metrikk vi kunne bruke for å evaluere hvor godt modellen presterte ved hjelp av et sett med test-datapunkter. I denne posten skal vi se på en annen, svært vanlig modell fra statistikken, men la oss først gå over problemet vårt enda en gang: Som du sikkert nå husker, har vi rollen som en karuselloperatør i et tivoli. Karusellen vi opererer krever at alle som tar den er over en gitt minimumshøyde (160 cm), men vi har mistet målebåndet vårt og har kun en vekt som hjelpemiddel.
La oss igjen se på dataen vår:
Her plotter vi vekt (x-aksen) mot høyde (y-aksen).
Hvis vi virkelig prøver kan det kanskje se ut som om veldig mange av punktene ligger på en linje. Det kan nesten se ut som om punktente i utgangspunktet har ligget på en linje, men deretter blitt kastet av linjen i forskjellige retninger. Så kanskje vi kan modellere dataen vår som om den ligger på en linje? Hvis vi bruker en linje som modell kan vi, når vi får en ny vektmåling, flytte oss på x-aksen til vi kommer til vekten vi har målt og deretter flytte oss opp langs y-aksen til vi treffer linjen vår. Vi kan så se inn på y-aksen hvor langt opp vi kom og der har vi høyden modellen vår predikerer!
Under har jeg illustrert fremgangsmåten i en figur. Her måler vi en vekt på 70.0 kg: Steg 1: Start fra 70 på x-aksen og beveg deg vertikalt til du treffer den blå linjen. Steg 2: Når du har truffet linjen beveger du deg direkte horisontalt til du treffer y-aksen. Hvor langt opp du kom på y-aksen er modellens prediksjon, her ca 157.5 cm.
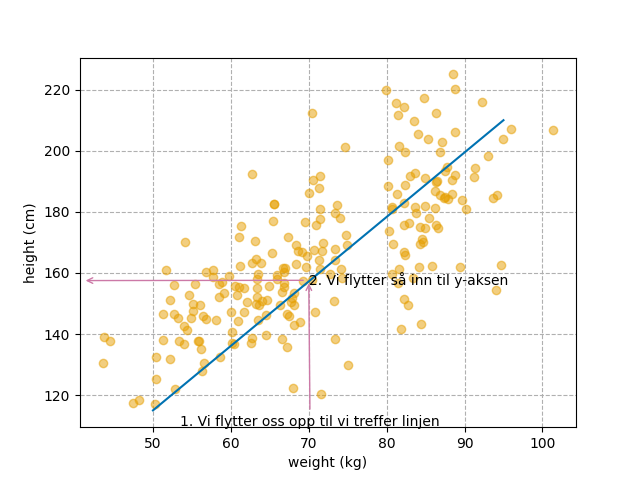Her ser vi hvordan vi starter fra en måling på 70 kg og finner høyden på ca. 157.5 cm.
Dette virker jo enkelt nok når vi har en bein linje å forholde oss til, men i det har jo ikke vi. Linjen er jo modellen vi skal bygge. Så hvordan gjør vi det?
Å tegne en linje
Før vi kan starte med å bygge en modell av en linje må vi ta en litt nærmere kikk på hva en linje faktisk er, eller hvordan vi kan definere en linje. Hva trenger vi for å kunne tegne en linje? Jo, vi trenger minst to punkter å tegne linjen gjennom. Hvorfor to? Jo du kan jo prøve å tegne en linje som går gjennom bare ett punkt. Hvor skal du starte? Du kan starte hvor som helst og trekke en linje gjennom punktet og du vil ha laget en linje. Du kan så starte en annen plass og trekke en ny linje gjennom punktet igjen. Da har du to linjer, som begge går gjennom det samme punktet, men de er åpenbart ikke den samme linjen. Så for at vi skal kunne definere én spesifikk linje i modellen vår trenger vi minst to punkter. Ett å starte fra og ett vi skal gjennom.
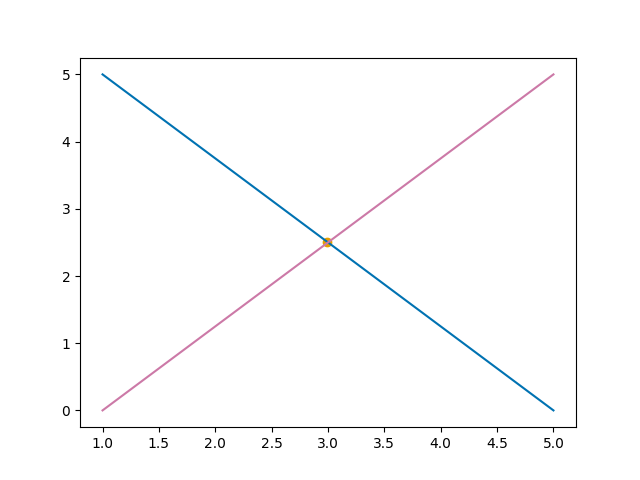To linjer går gjennom det samme punktet, men de er åpenbart ikke samme linje. Vi trenger derfor minst to punkter for å definere en linje.
Men kan vi bruke flere enn to punkter? Ja selvfølgelig! Under har jeg tegnet en linje definert av tre punkter:
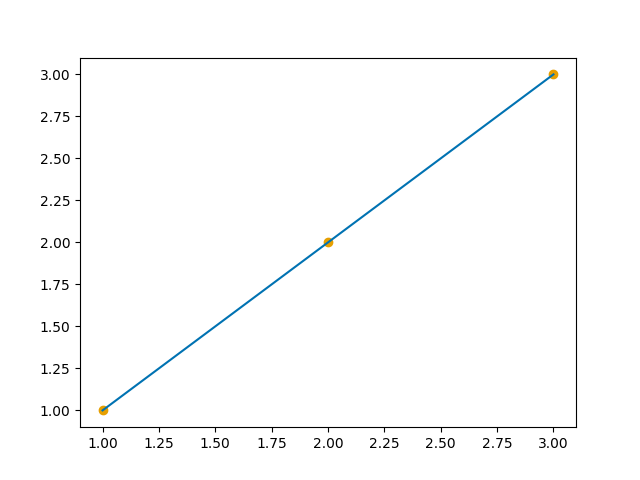Tre punkter kan definere samme linje.
Her har jeg brukt punktene (1, 1), (2, 2) og (3, 3). Det første tallet i hver parentes sier hvor punktet ligger langs x-aksen og det andre tallet i parentesen sier hvor punktet ligger langs y-aksen. Så det første punktet ligger ett steg ut på x-aksen og ett steg opp på y-aksen. Men hvordan vet vi at denne linjen er en 100% bein? Kan det ikke være at den er litt kurvet? En måte vi kan forsikre oss selv om det på er å beregne hvor mye linjen endrer seg, når vi flytter oss mellom punktene. Hvis denne endringen er lik mellom alle punktene vet vi at linjen vår er bein! Så la oss gjøre det.
Vi starter i det første punktet (1, 1) og flytter oss til neste punkt (2, 2). For å finne endringen langs x-aksen subtraherer vi x-verdiene fra hverandre, og for å finne endringen i y-aksen subtraherer vi y-verdiene fra hverandre. Hvis vi setter beregningen for endringen langs y-aksen i telleren og beregningen for endring langs x-aksen i nevneren i en brøk kan vi beregne den totale endringen for linjen: \(\frac{2 - 1}{2-1} = \frac{1}{1} = 1\)
Vi kan nå gjøre det samme fra punkt to (2, 2) til punkt tre (3, 3): \(\frac{3 - 2}{3-2} = \frac{1}{1} = 1\)
Endringen er 1 i begge tilfeller. Vi har en bein linje! Det vi har beregnet her er stigningstallet til linjene som ligger mellom punktene. Hvis dette stigningstallet er likt, vet vi at alle tre punkter ligger på den samme overordnede linjen. Stigningstallet defineres for en linje generelt slik:
\[\begin{equation} a = \frac{y_2 - y_1}{x_2 - x_1} \end{equation}\]Men her snublet vi over noe interessant. Jeg sa nettopp at hvis stigningstallet til linjen mellom punktene er likt, så må også punktene ligge på den samme overordnede linje. Det betyr at vi kan bruke stigningstallet, $a$, til å definere en linje. Men er det nok med bare stigningstallet? Nei, stigningstallet sier jo bare hvor mye linjen endrer seg når vi beveger oss langs x-aksen. Men det finnes uendelig mange linjer som endrer seg like mye. Under har jeg tegnet tre linjer. De har samme stigningstall, men er åpenbart ikke samme linje. Jeg har også inkludert y-aksen i svart.
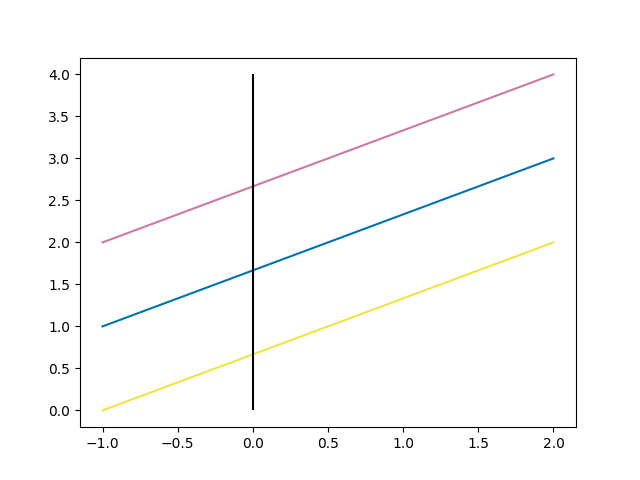Tre linjer med samme stigningstall.
Så vi trenger altså noe mer enn bare stigningstallet. Men hvis vi tar en ny titt på figuren over, så ser vi at selv om alle tre linjene har samme stigningstall, så krysser de y-aksen på forskjellige punkter. Kan vi bruke punktet hvor linjen krysser y-aksen sammen med stigningstallet til å definere linjen? Ja det kan vi faktisk! Vi kan definere en generell linje som:
\[\begin{equation} y = ax + b \end{equation}\]$a$ er da stigningstallet vi definerte i stad. $x$ er hvor langt langs x-aksen vi flytter oss og $b$ er hvor linjen krysses y-aksen. Denne definisjonen av en linje har du antakelig sett tidligere, men jeg syntes det var nyttig å bruke litt tid til å se på hvorfor denne definisjonen stemmer.
Hvilken linje gir den beste modellen?
Okay, så nå har vi kommet et godt stykke på veien, vi har mange datapunkter og vi vet hvordan vi kan definere en linje. Men nå kommer neste store utfordring. Hvordan finner vi den linjen som best beskriver dataen vår? Eller sagt på en annen måte. Hvordan finner vi den beste modellen, gitt dataen vår og at modellen er en bein linje?
Under har jeg tegnet tre linjer gjennom datasettet vårt. Hvilken av linjene passer dataen vår best?
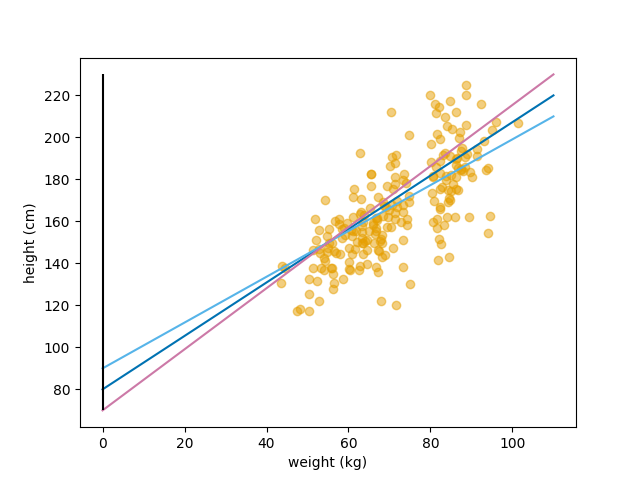Tre linjer, men hvilken passer dataen best?.
Kan vi kanskje si noe om hvor langt unna linjen vår er fra hvert datapunkt i datasettet vårt? Det burde jo kunne si noe om hvor bra linjen passer til dataen. Hvis vi finner avstanden mellom hvert datapunkt og linjen og legger sammen det, vil ikke den linjen som ha lavest summerte avstand også være den linjen som har passer dataen vår best? Dette er verdt å teste ut, men la oss starte med et noen få eksempeldatapunkter og et par linjer for å teste ut dette.
Vi starter med punktene:
- (1, 1.5)
- (2, 3)
- (2.5, 2.8)
- (3, 2)
Vi bruker også linjene:
- $y_1 = 1x + 0.0 = x$
- $y_2 = 0.66x + 0.5$
Under ser du punktene og linjene plottet:
To linjer, men hvilken passer dataen best?.
Ettersom vi kjenner punktenes posisjon og funksjonen som definerer hver av linjene, så kan vi også beregne avstanden mellom punktene og hver av linjene i vertikal retning. La oss også kalle denne avstanden residualet mellom punktet og linjen. Vi kan lage oss en python funksjon som gjør denne beregningen for oss:
1
2
3
4
5
def residual_between_point_and_line(point_x, point_y, line_a, line_b):
# Find the value of our line at the x-value of our point
line_y = line_a*point_x + line_b
# Subtract our line value from the y-value of our point
return line_y - point_y
Vi kan så kjøre denne koden for hver av linjene våre for å finne residualet for hvert punkt til hver av linjene. Under har jeg tegnet inn dette residualet:
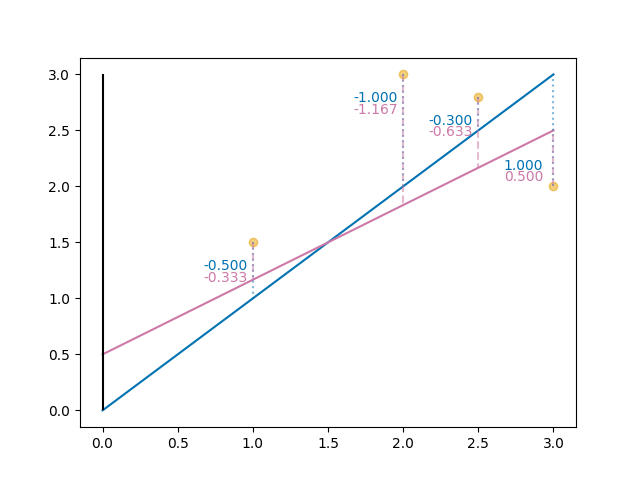To linjer og residualet mellom hvert punkt og hver av linjene. Residualet for den lilla linjen er en lilla stiplet linje, mens det er solid blå for den blå linjen.
Får den blå linjen finner vi altså residualene: \([-0.50, -1.000, -0.300, 1.000]\)
Og for den lilla linjen finner vi: \([-0.333, -1.167, -0.633, 0.500]\)
Vi kan nå summere disse residualene for å finne det totale residualet mellom alle punktene og hver av linjene:
For den blå linjen får vi da: \(-0.50 + (-1.000) + (-0.300) + 1.000) = -0.800\)
Og den lilla linjen: \(-0.333 + (-1.167) + (-0.630) + 0.500) = -1.633\)
Nå har du sikkert skjønt hva som kommer. Igjen har vi havnet i den situasjonen at vi summerer ulike fortegn og at de dermed utligner hverandre for å skape en kunstig lav sum. Dette er spesielt synlig i den blå linjen, hvor vi summerer 1.000 og -1.000. Disse to tallene utligner hverandre helt og gir oss et kunstig lavt residual. Det reflekterer rett og slett ikke hvor stor avstand det totalt sett er mellom punktene og linjen. Heldigvis kan vi igjen bare kvadrere hver av residualene før vi summerer og unngå det hele:
For den blå linjen får vi da: \(-0.50^2 + (-1.000)^2 + (-0.300)^2 + 1.000)^2 = 2.340\)
Og den lilla linjen: \(-0.333^2 + (-1.167)^2 + (-0.630)^2 + 0.500)^2 = 2.123\)
Og her ser vi plutselig at det er den lilla linjen som er nærmest punktene! Dette tallet kalles minste kvadrat (least square) og er en ekstremt vanlig måte kvantifisere hvor bra en linje passer til et sett med datapunkter. Så ved bruk av denne metoden kan vi si at den lilla linjen er den av de to linjene som passer dataen best.
Men hvordan finner vi den beste linjen?
Foreløpig har vi jo bare sett på hvordan vi kan avgjøre hvilken linje som passer dataen vår best, gitt at vi allerede har linjene definert. Men vi er jo egentlig ute etter å finne den linjen som passer best til dataen vår. Hvordan gjør vi det? Vi kunne jo startet å gjette på en linje og gradvis forbedre gjettingen vår ved å endre på verdiene for $a$ og $b$ til vi fant et sett med $a$ og $b$ hvor vi ikke lengre klarte å finne en bedre kombinasjon, men det er veldig tungvindt. La oss se om vi kan finne en bedre måte å gjøre dette på.
La oss starte fra minste kvadrat og definere det slik: \(\begin{equation} S(a, b) = r_1^2 + r_2^2 + r_3^2 + r_4^2 \end{equation}\)
Hvor $r_i$ er residualet mellom det $i$-te punktet og den $i$-te prediksjonen fra linjen vår $ax_i + b$.
Fra $a$ og $b$ til $\beta_1$ og $\beta_0$
Nå må jeg desverre gjøre noe ganske irriterende. For at det skal bli enklere å finne sammenhengen mellom det vi gjør fremover nå og generelle tekster i statistikk og maskinlæring må vi omdøpe $a$ og $b$. Som vi husker er $a$ stigningstallet til linjen og $b$ punktet hvor linjen krysser y-aksen. I statistikk er vi imidlertid veldig glad i det vi kaller parametre. Enkelt sagt er parametre deler av modellen vi kan justere. Som du sikkert husker, så ønsker vi nå å justere $a$ og $b$ slik at vi finner verdier for disse som gir oss den linjen som passer best til dataen vår. $a$ og $b$ er altså parametre i modellen vår. Desverre liker statistikere å gi parametre symboler fra det Greske alfabetet, så istedet for $a$ og $b$, bruker man helst $\beta_1$ og $\beta_0$. Vi endrer også rekkefølgen vi skriver uttrykket for en linje på, fra $y = ax + b$ til $y = \beta_0 + \beta_1 x$. Grunnen til dette er at vi gjerne ønsker å vektorisere funksjonene våre og da bruker $\vec{\beta}$ som utrykk. Det gjør det mulig for $\vec{\beta}$ å inneholde enda flere parametre enn $\beta_0$ og $\beta_1$, noe vi skal se at er veldig nyttig senere. Uheldigvis er vi ikke ferdige med det. I enkelte modeller, som i denne, kan vi også finne på å kalle parameterne koeffisienter også. Parametre og koeffisienter brukes ofte om hverandre i denne typen modell hvor vi tegner linjer.
Men la oss nå slå oss til ro med at vi har omdefinert uttrykket for linjen vår til: \(\begin{equation} y_i = \beta_0 + \beta_1 x_i \end{equation}\)
Tilbake til å finne den beste linjen
La oss returnere til oppgaven med å finne den beste linjen til dataen vår.
Så la oss først sette opp et ligningssystem som definerer den beste linjen ut fra de fire punktene våre. Husk at vi har punktene:
- (1, 1.5)
- (2, 3)
- (2.5, 2.8)
- (3, 2)
Vi kan da definere linjen som:
\[\begin{equation} \begin{aligned} \beta_0 + \beta_1 1 = 1.5 \\ \beta_0 + \beta_1 2 = 3 \\ \beta_0 + \beta_1 2.5 = 2.8 \\ \beta_0 + \beta_1 3 = 2 \end{aligned} \end{equation}\]Problemet her er at vi har et system med to ukjente, $\beta_0$ og $\beta_1$, men fire ligninger. Systemet er det vi kaller overdefinert og det finnes ingen eksakt løsning. Vi må derfor se på tilnærmede, approximate, løsninger. Hvis vi bruker residualer kan vi gjøre nettopp det: \(\begin{equation} \begin{aligned} \beta_0 + \beta_1 1 + r_1 = 1.5 \\ \beta_0 + \beta_1 2 + r_2 = 3 \\ \beta_0 + \beta_1 2.5 + r_3 = 2.8 \\ \beta_0 + \beta_1 3 + r_4 = 2 \end{aligned} \end{equation}\)
Dette kan vi skrive om til: \(\begin{equation} \begin{aligned} r_1 = 1.5 - (\beta_0 + \beta_1 1) \\ r_2 = 3 - (\beta_0 + \beta_1 2) \\ r_3 = 2.8 - (\beta_0 + \beta_1 2.5) \\ r_4 = 2 - (\beta_0 + \beta_1 3) \end{aligned} \end{equation}\)
Hvis vi nå putter dette inn i minste kvadrat formelen vår fra tidligere får vi: \(\begin{equation} \begin{aligned} S(\beta_0, \beta_1) = r_1^2 + r_2^2 + r_3^2 + r_4^2 \\ = [1.5 - (\beta_0 + \beta_1 1)]^2 + [3 - (\beta_0 + \beta_1 2)]^2 + [2.8 - (\beta_0 + \beta_1 2.5)] + [2 - (\beta_0 + \beta_1 3)]^2 \\ = 4 \beta_0^2 + 17 \beta_0 \beta_1 - 18.6 \beta_0 + 20.25 \beta_1^2 - 41 \beta_1 + 23.09 \end{aligned} \end{equation}\)
Den beste løsningen blir da den som minimerer $S$ med hensyn til $\beta_0$ og $\beta_1$. Vi finner dette minimumet ved å sette partialderivatene til 0: \(\begin{equation} \begin{aligned} 0 = \frac{\delta S}{\delta \beta_0} = 8 \beta_0 + 17 \beta_1 - 18.6 \\ 0 = \frac{\delta S}{\delta \beta_1} = 17 \beta_0 + 40.5 \beta_1 - 41 \\ \end{aligned} \end{equation}\)
Dette systemet har løsningen $ \beta_0 \approx 1.61$ og $\beta_1\approx 0.34$. Så den beste linjen til disse fire datapunktene er: \(\begin{equation} Y = 1.61 + 0.34 X \end{equation}\)
Linær regressjon med “Ordinary Least Squares” (OLS):
Dette var veldig tungvindt og mye styr for å finne en linje for fire datapunkter, jeg skal innrømme at jeg heller ikke orker å beregne dette for hånd. I stedet brukte jeg WolframAlpha for å hjelpe meg. Men hvordan blir dette når vi har hundrevis av datapunkter? Da er ikke denne metoden med wolfram alpha så hjelpsom heller, siden vi må definere hele ligningssystemet med hundrevis av ligninger. Heldigvis, finnes det hjelpemidler som kan ta hele jobben for oss:
1
2
3
4
5
6
import statsmodels.api as sm
X = sm.add_constant(points_x)
y = points_y
model = sm.OLS(y, X).fit()
print(model.summary())
Ved å kjøre denne koden får vi ut:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.169
Model: OLS Adj. R-squared: -0.246
Method: Least Squares F-statistic: 0.4080
Date: Mon, 12 Jan 2026 Prob (F-statistic): 0.588
Time: 06:57:11 Log-Likelihood: -3.2990
No. Observations: 4 AIC: 10.60
Df Residuals: 2 BIC: 9.371
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 1.6086 1.188 1.354 0.308 -3.501 6.718
x1 0.3371 0.528 0.639 0.588 -1.934 2.608
==============================================================================
Omnibus: nan Durbin-Watson: 1.991
Prob(Omnibus): nan Jarque-Bera (JB): 0.517
Skew: 0.125 Prob(JB): 0.772
Kurtosis: 1.256 Cond. No. 8.07
==============================================================================
Her er det, det som står under “coef” kolonnen vi skal se på. Her møter vi igjen uttrykket koeffisienter. Denne kolonnen holder altså koeffisientene, eller parameterne for denne modellen. Her korresponderer “const” til $\beta_0$ og x1 til $\beta_1$. Legg merke til at vi finner igjen nøyaktig samme verdier som vi beregnet oss frem til for hånd! Så hva er dette her? Jo dette er det som kalles minste kvadraters metode for regresjon (Ordinary Least Squares (OLS) Regression). Dette er kanskje den aller mest kjente modellen i statistikk og maskinlæring. Det den gjør er nettopp å finne den beine linja som passer best til datapunktene våre ved å bruke nøyaktig den metoden vi utførte for hånd over. Den gjør det imidlertid lynraskt ved hjelp av en datamaskin. Det gjør at svaret kommer lynraskt!
Tilbake til karusellproblemet vårt
Nå kan vi bruke denne metoden til også å finne den beste linja til datapunktene våre i karuselldataen:
1
2
3
4
X_carousel = sm.add_constant(df_w2h.weight)
y_carousel = df_w2h.height
model = sm.OLS(y_carousel, X_carousel).fit()
print(model.summary())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
OLS Regression Results
==============================================================================
Dep. Variable: height R-squared: 0.525
Model: OLS Adj. R-squared: 0.523
Method: Least Squares F-statistic: 242.2
Date: Mon, 12 Jan 2026 Prob (F-statistic): 2.81e-37
Time: 06:57:30 Log-Likelihood: -925.76
No. Observations: 221 AIC: 1856.
Df Residuals: 219 BIC: 1862.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 71.9374 6.120 11.755 0.000 59.876 83.999
weight 1.3154 0.085 15.564 0.000 1.149 1.482
==============================================================================
Omnibus: 3.096 Durbin-Watson: 1.986
Prob(Omnibus): 0.213 Jarque-Bera (JB): 3.386
Skew: 0.055 Prob(JB): 0.184
Kurtosis: 3.596 Cond. No. 411.
==============================================================================
Så OLS forteller oss at den linjen som passer best til karuselldataen vår er: \(\begin{equation} \text{høyde} = 71.94 + 1.32 \times \text{vektmåling} \end{equation}\)
Den linja ser slik ut: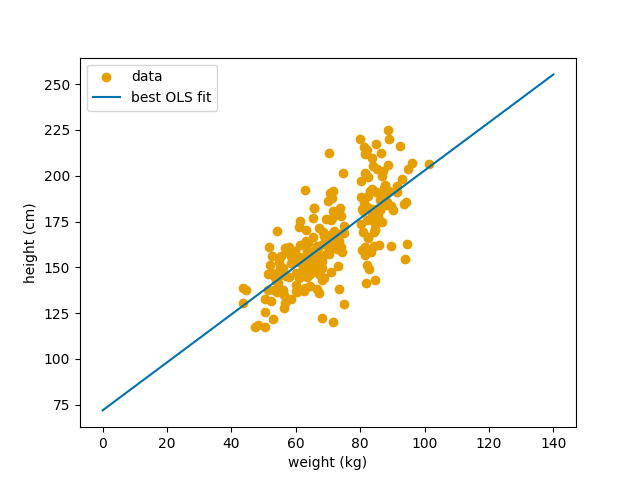 
Her ser vi den beine linja som passer dataen vår best.
Så hvordan presterer denne modellen i forhold til $k$-nærmeste nabo modellen som vi utviklet i forrige post? For å kunne svare på det, må vi først separere ut det samme test-datasettet fra dataen vår, slik vi gjorde i forrige post. Deretter kan vi finne den beste linjen til datasettet vårt uten test-dataen, for så å evaluere den linjen på test-dataen vår. La oss gjøre det nå:
1
2
3
4
5
6
7
test_data = pd.DataFrame(df_w2h.sample(int(len(df_w2h)*0.1), random_state = rng))# Sample verification data
train_data = df_w2h.drop(test_data.index) # Remove the sample from the data used to generate predictions
X_carousel_train = sm.add_constant(train_data.weight)
y_carousel_train = train_data.height
model = sm.OLS(y_carousel_train, X_carousel_train).fit()
print(model.summary())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
OLS Regression Results
==============================================================================
Dep. Variable: height R-squared: 0.502
Model: OLS Adj. R-squared: 0.499
Method: Least Squares F-statistic: 198.5
Date: Mon, 12 Jan 2026 Prob (F-statistic): 1.22e-31
Time: 06:57:58 Log-Likelihood: -840.29
No. Observations: 199 AIC: 1685.
Df Residuals: 197 BIC: 1691.
Df Model: 1
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
const 73.7134 6.649 11.087 0.000 60.602 86.825
weight 1.2953 0.092 14.090 0.000 1.114 1.477
==============================================================================
Omnibus: 1.915 Durbin-Watson: 1.908
Prob(Omnibus): 0.384 Jarque-Bera (JB): 1.713
Skew: 0.016 Prob(JB): 0.425
Kurtosis: 3.453 Cond. No. 409.
==============================================================================
Vi kan da bruke modellen vår til å gjøre prediksjoner og sammenligne prediksjonene med test-dataen vår for å beregne avstanden på samme måte som vi gjorde for $k$-nærmeste nabo modellen:
1
2
3
test_predictions = [73.71+1.30*wt[1].weight for wt in test_data.iterrows()]
# Calculate root squared average distance
print(rms_diff(test_predictions, test_data))
Da finner vi:
1
9.922
OLS modellen vår har bommer i gjennomsnitt med 9.922 cm når den skal predikere høyden ut fra en vektmåling. Sammenlignet med 5-nærmeste nabo modellen vår, som bommet med 16.9 cm i gjennomsnitt, er dette en drastisk forbedring!
Nå har vi gjort store fremskritt synes jeg. Vi har funnet en modell som virker godt egnet til å hjelpe oss med å avgjøre om vi skal la folk ta karusellen vår eller ikke. Jeg tror derfor dette er et godt sted å avslutte denne bloggposten. Men ikke misforstå, vi er langt unna ferdig!
Kode
Koden for denne posten finnes her.
Endringslogg
Under følger en endringslogg som viser hvilke deler av denne posten som er endret til hvilket tid. Enkle skrivefeil og den slags ting vil ikke bli logget, men jeg vil etterstrebe å logge alle meningsfulle endringer i posten.